How is return on investment calculated?

Calculating the return on investment portfolio is an essential element for any investor and is one of the main objectives when making the decision to invest.

Despite the importance of calculating the portfolio's return, it is quite common on several platforms (banks or investment companies) not to be able to obtain the performance of the portfolio. The most normal thing is that only the statements with the positions at the end of each month or the accumulated return of each asset in the portfolio are available, but not in an integrated way, that is, taking into account the total portfolio (at least the portfolio that the investor has in that financial intermediary), the dates of purchase and sale, income received, time elapsed, costs and taxes paid, possible leverage or volatility and other performance measures.

It is therefore the responsibility and interest of the investor to provide the necessary resources to calculate the performance. This is because a complete assessment of the portfolio, at least periodically, is essential for decision-making and for analyzing the portfolio against market benchmarks or against defined objectives.

The approach we want to take here is just to calculate the return on the investment portfolio from the perspective of the individual investor, using different metrics and forms of presentation.

To contextualize, it is important to clarify that the calculation of profitability is more complex than it seems and can lead to wrong analyzes if we do not know what type of return is being presented.

 

Notes:

1. The words return and profitability are used indiscriminately in this article and with the same meaning.
2. We want to help you be a better investor and achieve your goals:

• We help you develop your Investment Policy Statement;
• We develop individual or group training on investments and savings;
• We quantitatively analyze your current portfolio with Future Analyzer's computational technology and finances;
• Request more information about the investment advisory service provided through Banco Invest.

 

Key elements to consider:

 

• The holding period return on investment is the total percentage return realized on an investment during the period in which we were invested or for the period we are analyzing.
• The return on investment can be calculated using the arithmetic return, the geometric return and the logarithmic return method.
• To calculate the average return on the portfolio (annual or monthly average return, for example) over a series of periods or through the cumulative total return, we use the return based on the arithmetic average or the return according to the geometric average. It is important to know which method to use, depending on the type of investment we make and the volatility, and it is also essential to take into account the capitalization effect of the “compound interest/return” (the effective return).
• The effective return of an investment over several periods and taking into account different amounts invested (the inflow or outflow of money), can be calculated using the TWRR (time-weighted rate of return) method - time-weighted rate of return - and MWRR (money-weighted rate of return) – rate of return weighted by the money invested.
• CAGR is the effective annual growth rate (return or profitability) of an investment while AARG is the linear annual growth rate based on the arithmetic return and without considering the capitalization effect.
• Return measures may also take into account leverage, taxes and transaction or management costs (Gross rate of return of fees and taxes or net of fees or taxes) and inflation (nominal rate of return or real rate of return).

 

Holding period return on investment

In general, the total return on investment in a given period can be calculated using the following arithmetic return formula for a single period of time (holding period return):

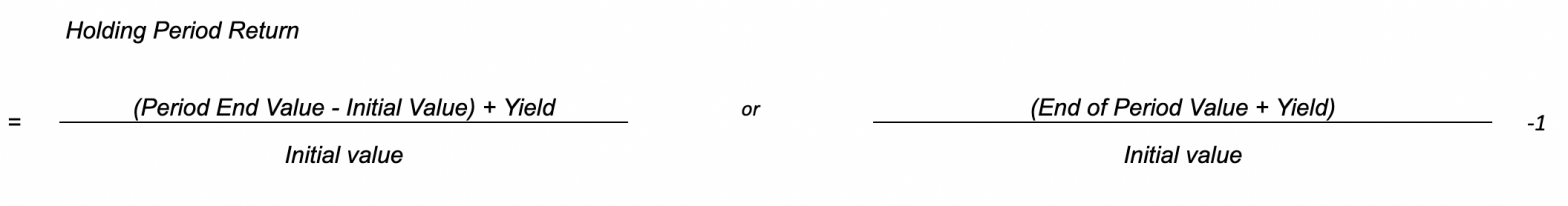
Financial assets typically produce two types of returns: the income return from interest or dividends and the return resulting from the rise or fall in the price of financial assets that lead to a capital gain or loss.

 

Total return = interest and dividend yield + price change

 

The term deposit, for example, generates only one type of return, the return resulting from interest. On the other hand, there are stocks that do not distribute dividends, so the return comes only from the variation in their quotation.

The total return means that we are taking into account the price variation, but also any income distributed in the portfolio, such as dividends and interest.

By period we can understand the period in which we held the investment or simply the period we defined for analysis. It is common to see situations where the returns from the beginning of the investment or the accumulated returns are presented. The period can be 1 hour, 1 day, 1 week, 1 month, 1 year, 3 years or other specific period.

 

Let's look at the following example:

Initial value of the portfolio: 1,000 euros

Final value of the portfolio after sale: 1,500 eur

Dividend received at the end of the period: 200 eur

The holding period return is equal = 7%

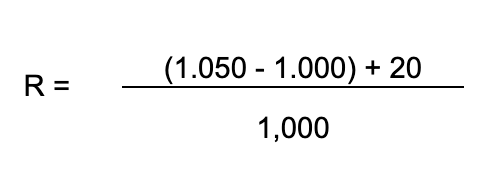
As mentioned above, this return is the arithmetic return, the simplest return to calculate. Alternatively, we could use the logarithmic return, which consists of the natural logarithm (ln) of the arithmetic return.

Keeping our attention on the arithmetic return, if the defined period is 6 months, to annualize it we would have to do:

Annualized holding period return = (1 + 7%) ^ (2) - 1 = 14.5%

Let's now imagine that the periodic returns for the last 3 months are known. In order to obtain the effective cumulative return for this 3-month period, we will have to take into account the capitalization effect of the 3 monthly returns. So,

Total return = (1 + R1) x (1 + R2) x (1 + R3) – 1, where R1, R2 and R3 are the 3 monthly periodic returns.

 

Exemplifying:

R1 = 1%; R2 = 2%; R3 = 1%

Total Return = (1 + 1%) x (1 + 2%) x (1 + 1%) - 1 = 4.05%, return for the 3 month period.

 

If, alternatively, we have an application that obtained a return of 2% in a period of 2 years and we want to know the return of the annual period, the result is not 1%. The result is close, but we will have to consider the compounding effect, so we do: Annualized Effective Return = (1 + 2%) ^ (1/2) – 1 = 0.995%.

In summary, we will then consider three types of return, taking into account the capitalization regime and the periodicity (single or multiple):

• Simple or arithmetic return - for a period, without compound capitalization;
• Compound or geometric return - for multiple periods, with compound capitalization;
• Continuous or logarithmic return - infinite and continuous periods, with compound capitalization.

As we will see in the next article, the simple periodic return is the basis for calculating the return for multiple periods, where we will use the arithmetic return and geometric return methods.

At this point it makes sense to also define the simple capitalization regime and the compound capitalization regime.

The simple capitalization return appears in several situations. It is the profitability that is disclosed when we see advertising for a term deposit rate or a bond issue and appears with the designation of nominal rate (TANB). It is a rate that does not presuppose the reinvestment of income.

The compounding return or geometric return takes into account the effects of periodic reinvestment of income and continuity over multiple periods. In a simple form, it is a return that takes into account “interest interest” or “compound interest”. Therefore, we call this cash return because it represents the effective return of the portfolio.

The interest rate is simple when the total amount of interest is calculated based only on the initial capital, that is, the rate is not levied on the amount of interest accrued periodically.

The interest rate is called compound when the total amount of interest results from the initial capital and also from the amount of interest accrued periodically.

In the following table we see an example of an investment of €10,000 with an annual interest rate of 7% and the respective results in each of the capitalization schemes.

To calculate returns for shorter periods such as hours or days, we can use logarithmic or continuous returns. One of the advantages of this type of return is that, for multiple time periods, you simply add the returns for each time period. However, for the sake of simplification, we will not delve into this type of return.

In the following articles you can delve deeper into this subject:

• The total, cumulative, average return over multiple periods
• The time weighted rate of return and the amount invested
• Other factors in the return analysis such as leverage, inflation, costs and taxes.