Como se calcula o retorno do investimento?

O cálculo do retorno da carteira de investimento é um elemento essencial para qualquer investidor e é um dos principais objetivos quando tomamos a decisão de investir. 

Apesar da importância do cálculo do retorno da carteira, é bastante comum em diversas plataformas (bancos ou empresas de investimento) não ser possível obter a performance da carteira. O mais normal é apenas estarem disponíveis os extratos com as posições no final de cada mês ou então a rentabilidade acumulada de cada ativo da carteira, mas não numa forma integrada, ou seja, tendo em consideração a carteira total (pelo menos a carteira que o investidor tem nesse intermediário financeiro), as datas de compra e venda, os rendimentos recebidos, o tempo decorrido, os custos e impostos pagos, a eventual alavancagem ou a volatilidade e outras medidas de performance.

É assim da responsabilidade e interesse do investidor providenciar os recursos necessários para calcular a performance. É que uma avaliação completa da carteira, pelo menos periodicamente, é fundamental para a tomada de decisões e para analisar a carteira face às referências de mercado ou face aos objetivos definidos. 

A abordagem que queremos fazer aqui vai apenas para o cálculo do retorno da carteira de investimento na ótica do investidor individual, utilizando diferentes métricas e formas de apresentação.

Para contextualizar, é importante esclarecer que o cálculo da rentabilidade é mais complexo do que parece e pode levar a análises erradas se não soubermos que tipo de retorno está a ser apresentado. 

 

Notas:

1. As palavras retorno, rendibilidade e rentabilidade são usadas neste artigo de forma indiscriminada e com o mesmo significado.
2. Queremos a ajudá-lo a ser melhor investidor e atingir os seus objetivos:

• Ajudamos a desenvolver a sua Declaração de Política de Investimento;
• Desenvolvemos formação individual ou em grupo sobre investimentos e poupança;
• Analisamos de forma quantitativa o seu portefólio atual com a tecnologia e finanças computacionais do Future Analyzer;
• Solicite mais informações sobre o serviço de consultoria para investimento, assegurado através do Banco Invest.

 

Elementos-chave a considerar

• O retorno periódico do investimento é o retorno total em percentagem realizado num investimento durante o período em que estivemos investidos ou referente ao período que estamos a analisar.
• O retorno do investimento pode ser calculado através do método do retorno aritmético, do retorno geométrico e do retorno logarítmico.
• Para calcularmos o retorno médio da carteira (rentabilidade média anual ou mensal, por exemplo) numa série de períodos ou através do retorno acumulado total, utilizamos o retorno com base na média aritmética ou o retorno de acordo com a média geométrica. É importante sabermos qual o método usar, dependendo do tipo de investimento que fazemos e da volatilidade, sendo também essencial ter em consideração o efeito capitalização do “juro/retorno composto” (o retorno efetivo).
• O retorno efetivo de um investimento durante vários períodos e tendo em consideração diferentes valores investidos (a entrada ou saída de dinheiro), pode ser calculado com recurso ao método da TWRR (time-weighted rate of return) – taxa de retorno ponderada pelo tempo - e MWRR (money-weighted rate of return) – taxa de retorno ponderada pelo dinheiro investido.
• O CAGR é a taxa de crescimento (retorno ou rentabilidade) anual efetiva de um investimento enquanto a AARG é a taxa de crescimento anual linear com base no retorno aritmético e sem considerar o efeito de capitalização. 
• As medidas de retorno podem ainda ter em consideração a alavancagem, os impostos e custos de transação ou de gestão (Taxa de retorno bruta de comissões e impostos ou líquida de comissões ou impostos) e a inflação (taxa de retorno nominal ou taxa de retorno real).

 

Retorno periódico do investimento

De uma forma geral o retorno total do investimento num determinado período pode ser calculado através da seguinte fórmula do retorno aritmético para um único período de tempo (holding period return):

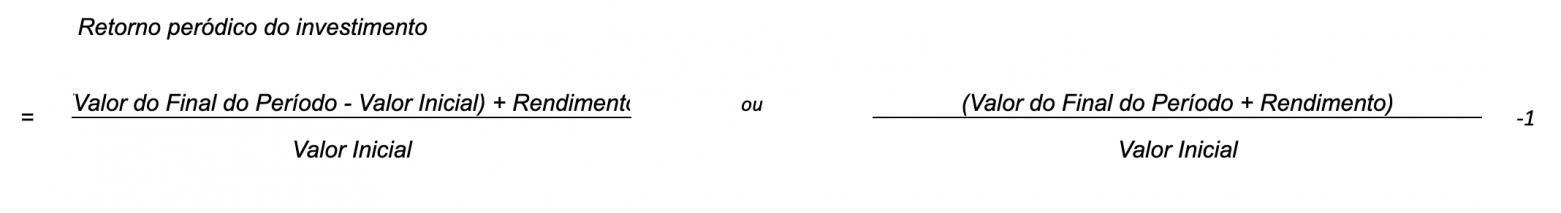
Os ativos financeiros normalmente produzem dois tipos de retorno: o retorno periódico proveniente de juros ou dividendos e o retorno resultante da subida ou descida do preço dos ativos financeiros e que conduzem a um ganho ou perda de capital.

 

Retorno total = rendimento de juros e dividendos + variação do preço

 

O depósito a prazo, por exemplo, gera apenas um tipo de retorno, o retorno resultante dos juros. Por outro lado, há ações que não fazem distribuição de dividendos, por isso, o retorno é proveniente apenas da variação da sua cotação.

O retorno total significa que estamos a ter em consideração a variação do preço, mas também os eventuais rendimentos distribuídos na carteira, como sejam os dividendos e os juros.

Por período podemos entender o período em que detivemos o investimento ou simplesmente o período que definimos para análise. É comum vermos situações onde são apresentados os retornos desde início do investimento ou os retornos acumulados. O período pode ser 1 hora, 1 dia, 1 semana, 1 mês, 1 ano, 3 anos ou outro período específico.

 

Vejamos o seguinte exemplo:

Valor inicial da carteira: 1.000 eur

Valor final da carteira após venda: 1.500 eur

Dividendo recebido no fim do período: 200 eur

O retorno do período é igual = 7%

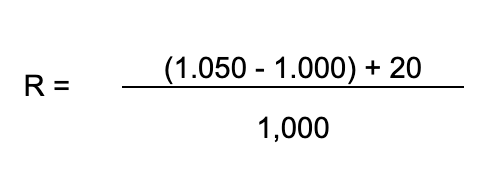
Como referimos acima, este retorno, é o retorno aritmético, o retorno mais simples de calcular. Em alternativa poderíamos utilizar o retorno logarítmico, que consiste no logaritmo natural (ln) do retorno aritmético.

Mantendo a nossa atenção no retorno aritmético, se o período definido for de 6 meses, para o anualizarmos teríamos de fazer: 

Retorno periódico anualizado = (1 + 7%) ^ (2) – 1 = 14,5%

Imaginemos agora que são conhecidos os retornos periódicos dos últimos 3 meses. Para obtermos o retorno acumulado efetivo deste período de 3 meses, teremos de ter em atenção o efeito capitalização dos 3 retornos mensais. Assim,

Retorno total = (1 + R1) x (1 + R2) x (1 + R3) – 1, onde R1, R2 e R3 são os 3 retornos periódicos mensais.

 

Exemplificando:

R1 = 1%; R2 = 2%; R3 = 1%

Retorno total = (1 + 1%) x (1 + 2%) x (1 + 1%) – 1 = 4,05%, de retorno para o período de 3 meses.

 

Se, em alternativa, temos uma aplicação que obteve uma rentabilidade de 2% num período de 2 anos e quisermos saber o retorno do período anual, o resultado não é 1%. O resultado é próximo, mas teremos de considerar o efeito da capitalização composta, então fazemos: Retorno Efetivo Anualizado = (1 + 2%) ^ (1/2) – 1 = 0,995%.

Resumindo, vamos considerar então três tipos de retorno, tendo em consideração o regime de capitalização e a periodicidade (única ou múltipla):

• Retorno simples ou aritmético - para um período, sem capitalização composta;
• Retorno composto ou geométrico - para vários períodos, com capitalização composta;
• Retorno contínuo ou logarítmico - períodos infinitos e contínuos, com capitalização composta.

Como vamos ver no próximo artigo, o retorno periódico simples é a base para calcularmos o retorno para múltiplos períodos, onde vamos utilizar os métodos do retorno aritmético e do retorno geométrico.

Nesta altura faz sentido definir também o regime o de capitalização simples e o regime da capitalização composta.

O retorno de capitalização simples aparece em diversas situações. É a rentabilidade que é divulgada quando vemos publicidade a uma taxa de depósito a prazo ou a uma emissão de obrigações e aparece com a designação de taxa nominal (TANB). É uma taxa que não pressupõe o reinvestimento do rendimento. 

O retorno de capitalização composta ou retorno geométrico tem em consideração os efeitos do reinvestimento periódico do rendimento e a continuidade por múltiplos períodos. Numa forma simples, é um retorno que tem em consideração os “juros de juros” ou “juro composto”. Por isso, designamos este retorno de efetivo pois representa o retorno efetivo da carteira. 

A taxa de juros é simples quando o valor total dos juros é calculado com base apenas no capital inicial, ou seja, a taxa não incide sobre o valor dos juros acumulados periodicamente.

A taxa de juros designa-se de composta quando o valor total dos juros é resultante do capital inicial e também sobre do valor dos juros acumulados periodicamente.

Na tabela seguinte vemos um exemplo de um investimento de 10.000 € com uma taxa de juro anual de 7% e os respetivos resultados em cada um dos regimes de capitalização.

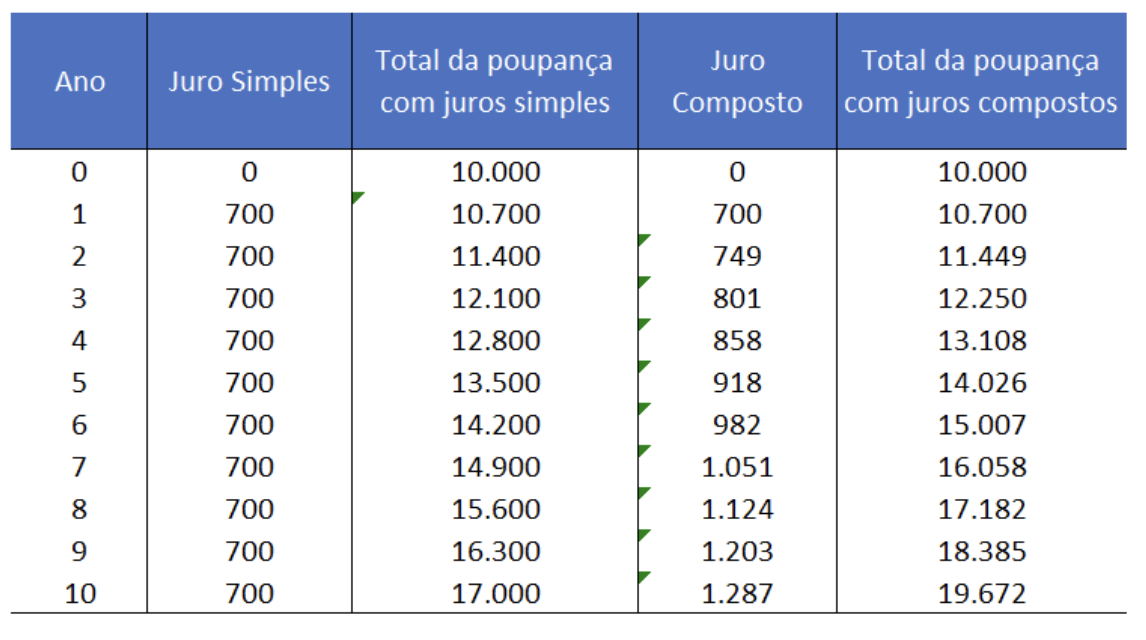
Para o cálculo de retornos de períodos mais curtos como horas ou dias, podemos utilizar o retorno logarítmico ou contínuo. Uma das vantagens deste tipo de retorno é que, para múltiplos períodos de tempo, basta somar os retornos de cada período de tempo. Contudo, por uma questão de simplificação, não vamos aprofundar este tipo de retorno.

 

Nos artigos seguintes pode aprofundar este assunto:

• O retorno total, acumulado, médio, em múltiplos períodos
• A taxa de retorno ponderada pelo tempo e pelo montante investido
• Outros fatores na análise do retorno como a alavancagem, a inflação, os custos e os impostos.